본 정리는 CS422-컴퓨터 구조 및 설계 : 하드웨어/소프트웨어 인터페이스. David A. Patterson, 존 헤네시 책을 바탕으로 하고 있음을 미리 알립니다.
캐시의 성능
CPU time = (CPU cycles + memory stall cycles) x CPU cycle time
memory stall cycles = 명령어의 수 x miss rate x miss penalty
CPU시간은 CPU가 프로그램을 수행하는 데 쓰이는 클럭 사이클과 메모리 시스템을 기다리는 데 쓰이는 클럭 사이클로 나누어 진다.
cache hit 되었을 때는 CPU cycles에 포함되고, cache miss 되었을 때는 memory 접근이 필요해지므로 memory stall cycle에 포함된다.
캐시로 성능을 높이는 방법은 misst rate와 miss penalty를 줄이는 방법 두가지이다.
Hit time도 성능에서 되게 중요한데, 캐시가 커지면 캐시의 큰 사이즈로 인해 접근시간도 늘기 때문에 잘 조절하여야 한다.
평균 메모리 접근 시간(Average memory access time (AMAT) )은 다음과 같이 정의할 수 있다.
AMAT = Hit time + Miss rate × Miss penalty
캐시의 실패 (miss rate)를 줄이기 위한 방법
지금까지는 직접 사상캐시만 봤는데 집합 연관 방식(set associative)을 이용한 캐시 구조를 한번 알아보자.
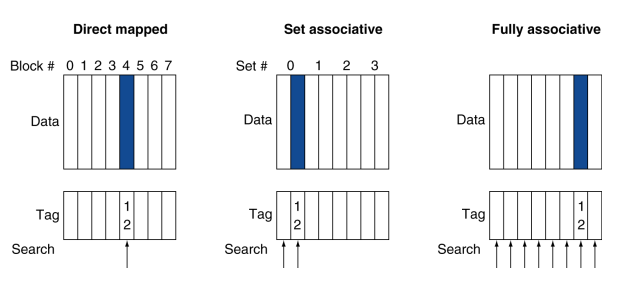
직접 사상캐시에서는 메모리 블록을 캐시에 넣을 때 각 블록이 캐시의 딱 한 곳에만 들어갈 수 있는 단순한 배치 방법을 사용하였다.
그러나 집합 연관 방식에서는 메모리 블록이 캐시의 딱 한곳이 아니라 한 블록이 들어갈 수 있는 자리의 개수가 고정되어 있어 해당하는 위치에 자유롭게 위치될 수 있다.
각 블록 당 n개의 배치 가능한 위치를 갖는 집합 연관 캐시를 n-way set associative cache라고한다.
이러한 관점에서 직접 사상캐시를 1-way associative cache라고도 할 수 있다.
추가로, 메모리 블록이 캐시의 어느 곳에나 위치할 수 있는 것을 완전 연관 (Fully associative) 방식이라고 하고 이러한 방식을 이용한 캐시를 Fully associative cache라고 한다.
완전 연관 방식에선 캐시에서 주어진 블록을 찾기 위해 캐시의 모든 블록을 탐색해야한다.
그렇다면 집합 연관 방식에서 메모리 블록을 캐시에 어떻게 대치 시키는지 알아보자.
그 전에 직접 사상캐시에선 어떻게 대치 시켰었는지 기억해보자.
(블록 주소) modulo (캐시 내에 존재하는 캐시 블록 수)
캐시가 캐시가 나타낼 수 있는 블록의 개수로 블록 주소를 나누어서 캐시에 각 자리에 대치되게 만들었다.
집합 연관 방식에선 캐시가 나타낼 수 있는 개수가 집합의 개수이다.
즉, 블록 주소를 집합의 개수로 나눈 나머지가 인덱스 값이 되어 대치된다.
(블록 주소) modulo (캐시 내에 존재하는 집합의 수)
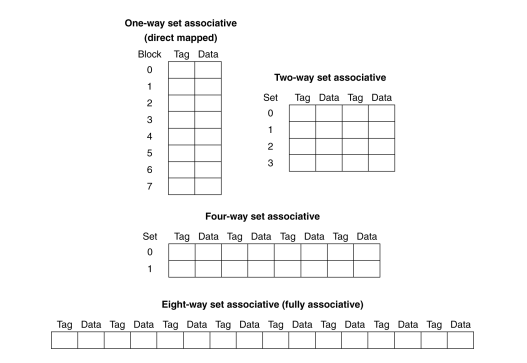
예시를 봐보자.
1word 크기를 갖는 블록 4개로 구성된 작은 세종류의 캐시(1. 직접 사상, 2. 2-way associative, 3. 4-way associative) 가 있다고하자.
이때, 블록 주소 0 8 0 6 8 순으로 블록을 참조한다면 miss의 횟수를 구해보자
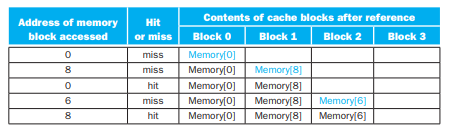
1. 직접 사상
블록의 개수가 4개이므로, 4로 나눈 나머지를 각각 구하면,

다음과 같이 되고, 이제 캐시의 각 자리에 값을 불러오면,
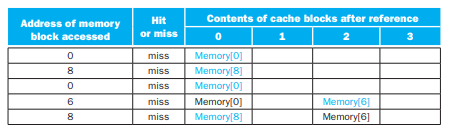
전부 miss가 나게 된다.
2. 2-way associative
집합의 개수가 4(블록의 개수) / 2 = 2 이므로, 블록의 주소를 2로 나눈 나머지를 구하면,

다음과 같이 되고, 이제 캐시의 각 자리에 값을 불러오면,

0 8 6 모두 한자리에 들어오게 되고 4번 miss가 나게 된다.
3. 4-way associative (fully associative)
4집합의 개수는 /4 는 1이므로 집합은 1개, 블록의 주소를 1로 나눈 나머지를 구하면 모두 0일 것이다.
즉 모두 하나의 잡합에 모두 들어가게 되고 캐시의 각 자리에 값을 불러오면,
다음과 같이 miss가 3번 나는 것을 알 수 있다.
miss가 나면 블록을 교체해주어야하는데, 이때 보통 최근에 이용되지 않았던 블록을 우선적으로 교체한다. -> LRU(Least-recently used)방식
그렇다면, 무조건 fully associative cache가 좋은 것이라고 할 수 있을까?
답은 '아니오' 이다.
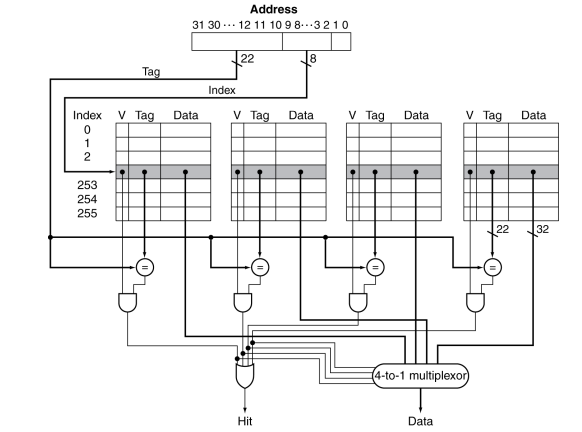
인덱스 값을 사용하여 하나의 집합에 접근하고, Tag를 사용하여 원하는 데이터가 맞는지 확인하는 과정을 거쳐야한다.
이때 n-way associative 라면 n개의 블록의 태그를 검사하여 같은 태그인지 확인하여야하기 때문에 이 n이 fully에 가까워 질 수록 이 검색의 비용이 증가하게 된다.
이때 검색은 선형 검색이 아니라 성능을 위해 병렬검색을 이용한다는 점을 참고!
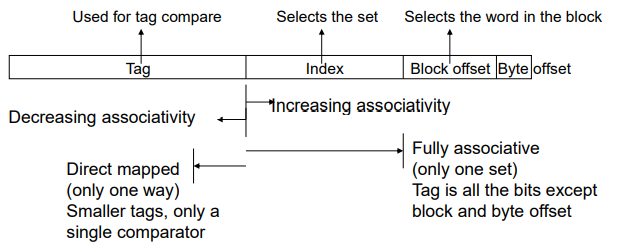
즉, n의 크기가 늘어날수록, index로 나타낼 수 있는 크기는 줄어들고, Tag를 이용하여 원하는 블록을 찾는 비용이 증가하게된다.
Fully associative라면 Tag만을 이용하여 모든 블록을 탐색해야한다.
정리해보면, n way associative cache를 사용하면 miss rate는 줄일 수 있지만, N개의 비교기와 MUX delay를 감수하여야 한다.
Multilevel Caches
프로세서의 빠른 클럭 속도와 상대적으로 점점 느려지는 DRAM (메인 메모리)의 접근 시간 사이의 차이를 더욱 줄이기 위해, 고성능 프로세서들은 캐시를 한계층 더 사용한다.

2차 캐시는 마이크로프로세서에 내장되어 있으며, 1차 캐시에서 실패가 발생할 때 접근된다.
2차 캐시가 원하는 데이터를 갖고 있으면 실패 손실은 2차캐시의 접근 시간이 되며, 이 값은 메인 메모리보다 훨씬 작기 때문에 성능이 매우 좋아진다.
보통 1차 캐시는 클럭 사이클의 단축이나 파이프라인 단계의 축소가 가능하도록 적중 시간 최소화에 초점을 맞추고, 2차 캐시는 메모리 접근 시간으로 인한 손실을 줄이기 위해 실패율을 줄이는데 초점을 맞춘다.
즉 단순하게는 메인 메모리보다 접근이 빠르지만 크기가 더 작은 계층 하나를 더 만든다고 생각하면 된다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [Chapter 5.6 컴퓨터 구조 및 설계] TLB (0) | 2022.07.31 |
|---|---|
| [Chapter 5.5 컴퓨터 구조 및 설계] 가상 메모리와 페이지 부재 (0) | 2022.07.30 |
| [Chapter 5.3 컴퓨터 구조 및 설계] 캐시 참조 실패와 성공의 처리 (0) | 2022.07.28 |
| [Chapter 5.2 컴퓨터 구조 및 설계] 직접 사상 캐시의 구조와 원리 (0) | 2022.07.26 |
| [Chapter 5.1 컴퓨터 구조 및 설계] 메모리 계층 구조 (0) | 2022.07.25 |



