본 정리는 CS422-컴퓨터 구조 및 설계 : 하드웨어/소프트웨어 인터페이스. David A. Patterson, 존 헤네시 책을 바탕으로 하고 있음을 미리 알립니다.
캐시의 구조
메모리 계층 구조에서는 상위 계층에서 먼저 데이터를 찾고 없다면 하위 계층에서 데이터를 요구하여 상위 계층에 채운다.
여기서 우리가 해결해야할 문제는 두가지다.
- 데이터가 캐시 내에 있는지 어떻게 알 수 있는가?
- 알 수 있다면, 어떻게 찾을 수 있는가?
각 워드가 캐시 내의 딱 한 장소에만 있을 수 있다면 워드가 캐시 내에 있는지 없는지를 바로 알 수 있다.
메모리의 각 워드에 캐시 내의 위치를 할당하는 가장 간단한 방법은 메모리 주소에 기반을 두고 할당하는 것이다.
이러한 캐시 구조를 바로 직접 사상( Direct mapped )라고 한다.
하위 계층(메모리)의 용량이 캐시에 비해 엄청나게 크기 때문에 캐시의 다른 장소에 모든 word를 다 직접 사상할 수 없다.
즉, 결국은 캐시에 같은 장소에 사상되는 word들이 생기게 된다.
직접 사상 캐시는 블록을 찾기 위하여 다음의 사상 방식을 사용한다.
(블록 주소) modulo (캐시 내에 존재하는 캐시 블록 수)

예를 들어 위와 같이 캐시의 블록수가 8 ( 2^3 ) 개라면, 각 word는 8로 나눈 나머지 하위 3bit를 기준으로 캐시에 사상된다.
즉, 캐시는 3bit만 표시할 수 있으므로, 하위 3bit만 이용하여 각 word를 캐시의 각 자리에 사상한 것이다.
이 하위 3bit를 보통 index라고 한다.
그렇다면, 요구하는 word가 캐시내에 있는지 없는지를 어떻게 알 수 있을까?
태그(tag)를 이용하면 이를 알 수 있다.
태그는 캐시의 인덱스로 사용되지 않은 주소의 윗부분 비트로 구성된다.
즉 위의 예시로 보면, 하위 3bit를 제외한 상위 2bit가 tag가 되는 것이다. 상위 2bit는 하위 3bit가 같다면 모두 다른 것을 볼 수 있다.
즉, memory의 00001 주소가 캐시로 올 때, 00(tag) 001(index)가 될 것이다.
프로세서가 맨처음 시작했을 때 캐시는 비어있을 것이고 이때의 태그 필드는 의미가 없을 것이다.
이럴 때 사용하는 것이 바로 유효비트(valid bit)이다.
정리하면, cache의 구조는 다음과 같다.
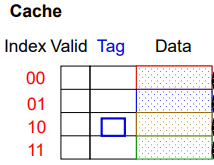
Hits vs Misses
- Read hits - 읽었을 때 캐시에 해당 데이터가 있다.
- Read misses - CPU를 멈추고 메모리로부터 데이터를 가져오고 재시작한다.
- write hits
- 캐시와 메모리에 있는 데이터를 바로 다시 쓴다 (write-through)
- 캐시에 있는 데이터만 우선 다시 쓰고 이후에 다시 메모리에 데이터를 업데이트한다.(write-back the cache later)
- Write misses - Read misses의 과정을 거쳐 데이터를 가져오고 write hits의 과정을 거친다.
22 26 22 26 16 3 18의 주소에 있는 데이터를 순서대로 프로세서가 시작 후 읽어온다고 가정해보자.

처음 시작은 캐시가 아예 비어있을 것이고, 22(10110)의 주소를 참조하면 인덱스 110을 먼저 읽고 valid가 N 이므로 miss가 일어나 캐시를 채울것이다

26도 마찬가지이다.

다시 22 26 을 읽으면 index와 tag 참조 후 hit가 일어나 변화가 없을 것이고, 16과 3도 위와 같이 miss가 일어날 것이다.
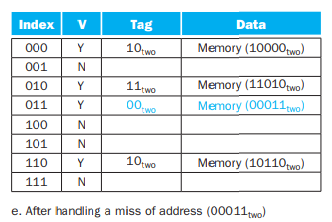
18(10010)을 읽을땐, index가 010 인 곳을 찾아가고 이때 tag 10으로 다르므로 miss가 일어나 캐시를 업데이트 할 것이다.
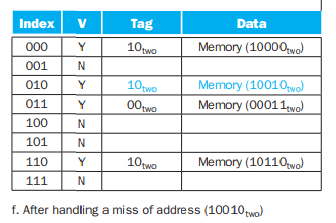
즉, 결론은 메모리 주소에서 cache의 size만큼 하위 비트가 index로 사상되고, 나머지 상위 bit는 tag로 사상되어진다는 것을 알면 된다.
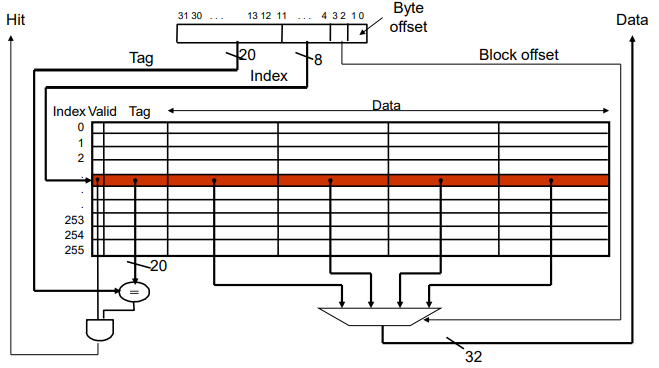
직접 사상 캐시의 구조
블럭이 1 word와 같고, cache의 size가 1024Byte라고 하자.
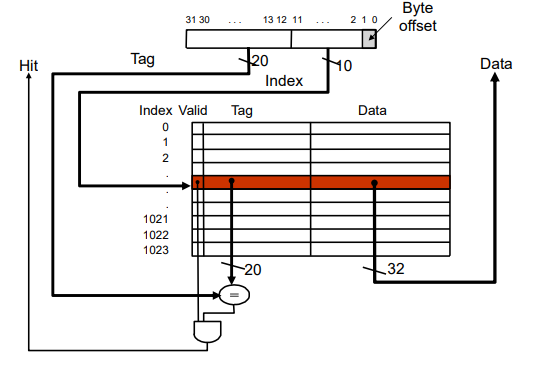
메모리 주소가 32bit라고 할때 메모리 주소는 1 word 4byte이므로 2bit (00 01 10 11)만큼 offset으로 최하위 bit를 갖고,
그 위에 cache의 size인 2의 10제곱 즉 10bit 만큼 index bit를 갖고 나머지 32 - 10 - 2 = 20 bit만큼 tag 비트를 갖는다.
Multiword Block Direct Mapped Cache
또 다른 예로, Multiword Block Direct Mapped Cache를 살펴보자.
캐시는 64block만큼 담을 수 있고 한 block의 크기는 16byte라고 하자. (위 그림과 다른 예시이다.)
64 = 2^6이므로 index는 6bit
1 block이 4word를 가지므로 offset은 16만큼 표시할 수 있는 4bit를 가져야한다.
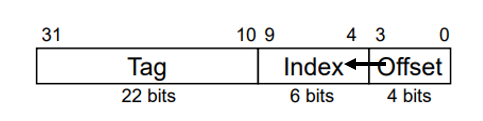
즉, 메모리 주소의 구조는 다음과 같이 될 것이다.
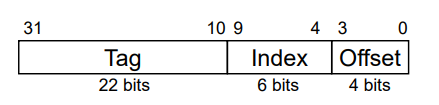
이때 1200의 주소를 맵핑한다고 하면 어떻게 될까?
우선 1200을 블럭단위 주소로 나타내기 위해 16으로 나누어준다.
1200/16 = 75.xxx
이제 이것을 캐시의 인덱스 사이즈인 64로 나누면 나머지가 tag 몫이 index가 되는 것이다.
이렇게 하나의 블록에 여러 word를 담아내는 것을 Multiword Block Direct Mapped Cache라고 한다.
Multiword Block Direct Mapped Cache는 block이 더 넓은 범위를 나타내여 Spatial Locality의 이점을 더욱 살릴 수 있다.
0 참조 miss 후에 1 주소를 참조한다고 할때 block이 2word만 포함한다고 하여도 1에서는 hit를 할 수 있는 것이다.
그렇다면 block의 size가 엄청나게 커지면 miss rate도 매우 줄지 않을까?
답은 No이다.
cahce size는 한정적이지 않기때문에 Block size가 증가하면
cache의 index가 줄어들기도 하고,
더 많은 블록을 가져와야하기 때문에 miss penalty가 더 증가하기도 하기 때문이다.
Cache Field Sizes
위에서 알게된 캐시의 구조로 캐시가 포함하고 있는 전체 bit 수를 구해보자.
주소는 32bit byte address라고 하고, 2^n 블록만큼 cache가 저장할 수 있다고 하자.
또 한 블록은 2^m word 만큼의 크기를 갖고 있다고 가정하자
그러면 2^n 만큼의 블록을 가지고 있다는 말이므로,
2^n X(block size + tag field size + valid field size)를 하면 캐시가 포함하고 있는 전체 bit 수를 알 수 있다.
Tag field size는 위에서 했던 방식대로, 32-n(index bit) - (m+2)(word byte offset)으로 구할 수 있다.
block size는 1word에 총 32bit가 필요하므로 32 x 2^m해주면 된다.
valid bit는 1bit이다.
예를 들어, 캐시가 16KB 만큼의 데이터를 저장할 수 있고, 4 word per block일 때 cache에 필요한 총 bit 수는 얼마일지 한번 구해보자.
16000KB -> 2^14
n은 14 m은 2이므로,
2^14 x (2^2 x 32(1word는 4byte이므로 4x8 bit만큼 1word에 필요하다) + (32-14 - 4) + 1)
가 될것이다.



