본 정리는 CS422-컴퓨터 구조 및 설계 : 하드웨어/소프트웨어 인터페이스. David A. Patterson, 존 헤네시 책을 바탕으로 하고 있음을 미리 알립니다.
IEEE 754 FP는 다음과 같은 반올림 모드를 갖고 있다.
- Always round up (toward +∞)
- Always round down (toward -∞)
- Truncate
- Round to nearest even
이러한 반올림 모드가 필요한 이유는

다음과 같이 F field가 23bit로 제한되어있기 때문에 해당 bit보다 더 소수 자리 수가 큰 수를 표현하기 위함이다.
현재의 부동소수점 표현 방식에선 거의 Round to nearest even를 사용한다.
Always round up
항상 올림을 뜻한다.
1.0011111001 을 소수 셋째자리까지 표현한다고 생각하면, 뒤에 수가 어떻든 1.010으로 올림된다.
Always round down
항상 내림을 뜻한다.
1.0011111001 을 소수 셋째자리까지 내림한다고 생각하면, 뒤에 수가 어떻든 1.001으로 내림된다.
Truncate
자름을 뜻한다.
뒤에 수가 어떻든 표현하고 싶은 수 외의 수는 모드 자른다.
1.0011111001 을 소수 셋째자리까지 자른다고 생각하면, 뒤에 수가 어떻든 1.001으로 잘린다.
Round to nearest even
우리가 흔히 생각하는 반올림이다.
위의 예시대로 올림 혹은 내림하면 모든 수는 한쪽 방향으로 치우쳐질 수 밖에 없기 때문에 나온 방식이다.
소수에서의 반올림은 조금 더 복잡하다.
우선, 내가 만약 1.0011011001을 소수 셋째 자리까지 표현하려고 했다고 해보자.
이 수는 1.001보단 크고 1.010보단 작은 수 이므로 둘 중 하나로는 반올림 되어야만 한다.
소수 네번째 자리부터 하나씩 차례로 Guard bit, Round bit, Sticky bit을 정한다.
즉, 1.001 1(G) 0 (R) 1(S) ... 이 될 것이다.
Guard bit
G가 0이면 1.0010...이 되고 이는 자명하게 내림쪽에 가까운 수(1.001) 이므로 Round bit Sticky bit 관계 없이 내림 해준다. 즉, 위의 예에서 G가 0이라면 R S 상관 없이 1.001이 되는 것이다. 만약 G가 1이라면 Round bit Sticky bit까지 확인 해야한다.
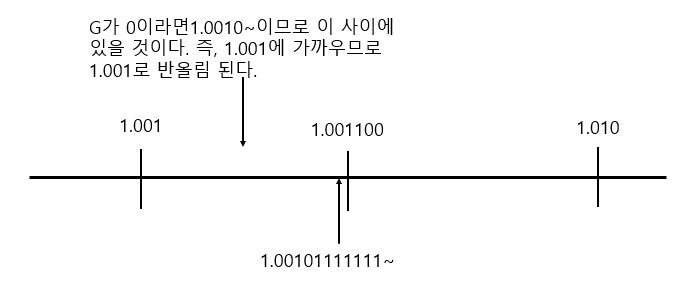
Round bit
G가 1일 때, 확인되는 bit이다. G와 비슷하게 만약 Round bit가 1이라고 하면, G가1 Round bit이 1이라면 1.00111.. 이고, 이는 1.001 보단 1.010 쪽에 조금 더 가까운 수 이므로, 올림이 된다. 즉 G가 1이고 R이 1이라면 올림이 되고, R이 0이라면 Sticky bit 까지 확인 하여야만 한다.

Sticky bit
G가 1이고 R이 0일 때 확인되는 bit이다. 이 bit는 특이하게 해당 bit만 확인하는게 아니라 뒤쪽에 나오는 모든 bit을 확인한 뒤에 1이 한번이라도 나오면 해당 bit도 1이 된다. 한번도 나오지 않는다면 해당 bit은 0이 된다.
1일때는 1.001101로 자명하게 1.010 쪽에 조금 더 가까운 수 이므로, 올림이 된다. 그러나 sticky bit이 0이라면, GRS가 100이되어 짝수의 방향으로 내림 혹은 올림 된다. (맨 마지막 bit 즉 lsb가 0이 되는 방향이 부동 소수점 표현에서 짝수를 의미한다.)


짝수의 방향이 약간 헷갈릴 수도 있는데 위의 예시에서, 만약 1.001이 1.010 이었고, 1.010이 1.011이었다면
GRS가 각각 100으로 1.010100인 수를 셋째짜리까지 반올림하려할 때, 1.010으로 반올림 된다는 것이다.
결국 이러한 반올림은 single precison이라고 생각한다면, 소수 23번째 자리까지만 나타낼 수 있으므로
해당 23번째 자리 이후까지 긴 소수에서 이런 반올림이 필요로 하다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [Chapter 3.7 컴퓨터 구조 및 설계] 부동 소수점 곱셈 (0) | 2022.07.15 |
|---|---|
| [Chapter 3.6 컴퓨터 구조 및 설계] 부동 소수점 덧셈 (0) | 2022.07.15 |
| [Chapter 3.4 컴퓨터 구조 및 설계] 부동소수점 표현 Normalized Denormalized Form (0) | 2022.07.13 |
| [Chapter 3.3 컴퓨터 구조 및 설계] 2진수 나눗셈, 나눗셈 하드웨어 (0) | 2022.07.12 |
| [Chapter 3.2 컴퓨터 구조 및 설계] 2진수 곱셈, 곱셈 하드웨어 (0) | 2022.07.12 |



