알고리즘을 풀다보면 그래프를 탐색해야하는 상황이 많이 발생한다.
그래프를 탐색하는 방법에는 크게 깊이 우선 탐색 (DFS)과 너비 우선 탐색 (BFS)가 있다.
두개의 알고리즘을 그림으로 보면 다음과 같다.
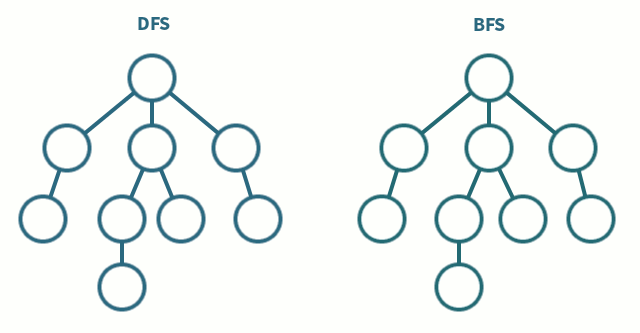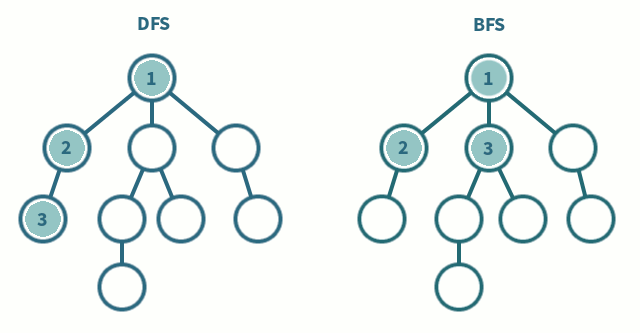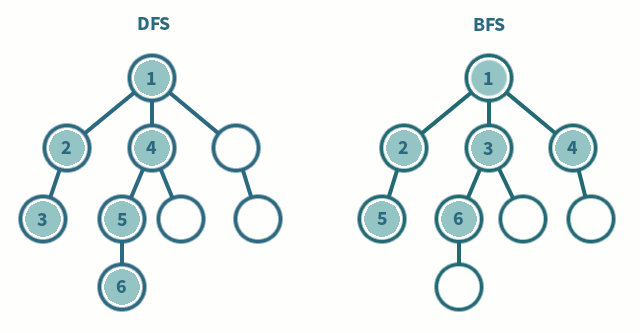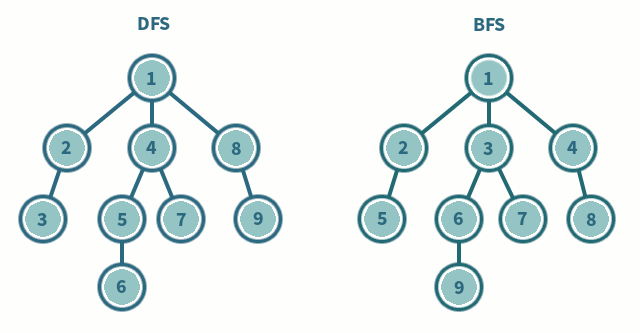
1. 깊이 우선 탐색 (DFS)
✅ 깊이 우선 탐색의 개념
한 노드로 부터 시작해서 다음 분기(다른 경로)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식을 말한다.
예를 들어서, 미로찾기를 한다고 가정해보자.
최대한 한 방향으로 가다가 해당 방향의 막다른 길에 다다랐을때, 다시 갈림길로 돌아와서 다른 경로를 똑같이 탐색하고, 이를 탈출구를 찾을 때까지 반복하는 것이 바로 DFS 깊이 우선 탐색이다.
그런데, 만약 잘못 선택한 경로가 올바른 경로에 비해 매우 깊은 (시간이 많이 걸리는) 경로라면??
매우 비효율적인 알고리즘이 될 것이다.
주로, 스택 혹은 재귀함수를 이용해서 구현한다.
정리해보면,
1. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택할 수 있다.
2. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 구현하기에 간단하다.
3. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
2. 너비 우선 탐색 (BFS)
✅ 너비 우선 탐색의 개념
한 노드로 부터 시작해서 인접한 노드부터 모두 탐색하고 이후에 그 인접한 노드의 인접한 노드를 방문하고 ... 을 반복하는 탐색 방식을 말한다.
즉, 최단경로를 찾을 때 매우 유용하다
주로, 큐를 이용해서 구현한다.
3. 언제 BFS를 쓰고, 언제 DFS를 써야할까?
문제 유형들에 따라 쭉 정리해보면,
1. 모든 정점을 방문해야할때,
무엇을 쓰든 상관이 없다.
둘의 시간 복잡도는 인접 리스트라 가정했을때, O(N(노드의 개수) + E(간선의 개수))로 동일하기 때문이다.
2. 최단 경로를 구해야할 때,
위에서 설명했듯,
DFS로 탐색 시 탐색한 경로가 무조건 최단경로라는 보장이 없어서, 여러번 많은 경로를 탐색하여야하는 반면,
BFS로 탐색 시 먼저 찾아지는 해답이 곧 최단거리이기 때문이다.
3. 그래프에서 그룹을 나눠야할 때,
사실 모든 정점을 방문해야하는 것과 다름 없겠지만,
나는 구현 상의 편의로 BFS를 주로 사용한다.
(BFS는 visited 배열을 사용하여 이미 방문한 노드는 안가는 것을 기정 사실화 하기 때문에, 모든 노드를 탐색하면서 visited면 BFS를 하고, 아니면 그냥 pass해주면 BFS를 통해 하나의 동일한 그룹을 얻어낼 수 있다.)
4. 다양한 경로 중 하나를 선택해야할 때,
예를 들어, 집부터 우체국까지 경로를 구해야하는데, 경로에 신호등이 없는 경로를 찾는 문제가 될 수 있겠다.
BFS는 경로를 가지진 못하므로 DFS를 선택하여야한다.
4. BFS,DFS 파이썬 코드
BFS 알고리즘은 보통 FIFO인 큐를 사용하는데 파이썬엔 deque() 자료구조를 주로 이용한다.
def bfs(r,c):
q = deque()
##해당 노드부터 탐색을 시작하여야 하므로 큐에 추가
q.append([r,c])
##무시해도 됨. 탐색한 노드들을 저장할 배열
team = []
team.append([r,c])
while len(q) != 0:
##큐에서 탐색한 노드를 제거
y,x = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
##예외처리를 통과한 인접한 노드들을 탐색
if nx >= 0 and nx < N and ny >= 0 and ny < N and not visited[ny][nx]:
if L <= abs(country[ny][nx] - country[y][x]) and abs(country[ny][nx] - country[y][x]) <= R:
visited[ny][nx] = True
##탐색한 노드의 인접한 노드들을 접근하기 위해 큐에 다시 추가
q.append([ny,nx])
team.append([ny,nx])
return team갈 수 있는 곳의 노드(같은 레벨의 노드)들은 deque에 append()하고 그 곳을 방문 했을 때, deque에서 제거해줌으로써 그래프를 탐색할 수 있게 된다.
더이상 갈 수 있는 노드가 없을 때 전부 popLeft()되어 함수가 종료된다.
DFS 코드
DFS는 주로 재귀 함수 형식 혹은 stack으로 구현하는데 나는 재귀 함수로 구현해보았다.
def dfs(depth,M,st,order,s):
if depth == M:
##여러가지 처리
##s부터 시작하는 이유는 순서를 부여하기 위함
for i in range(s,len(order)):
##이미 방문한 노드 방문 안하게끔! 없으면 자기 자신 노드도 다시 방문한다.
if not visited[i]:
visited[i] = True
temp = st +order[i]
dfs(depth+1,M,temp,order,i+1)
visited[i] = False
1. s부터 시작함으로써 무조건 오름차순(배열에 저장된 순)으로 탐색할 수 있게된다.
ex) [1,2,3,4] 배열에서 순서대로 숫자를 뽑을 때, 11 12 13 14 22 23 24 ... 형식으로 뽑아올 수 있다.
2. vistited 배열을 사용함으로써 자기 자신 노드를 재방문안할 수 있다,
ex) [1,2,3,4] 배열에서 순서대로 숫자를 뽑을 때, 12 13 14 21 23 24 ... 형식으로 뽑아올 수 있다.
한번 쭉 생각하면서 재귀함수가 어떻게 돌아가는지 이해해보면 DFS를 이해하기에 더 쉬울 것이라고 생각이든다.
주석을 보면서 천천히 이해 해보기를 바란다.
BFS와 DFS는 코딩 테스트에서 주로 나오는 그래프 문제에서 유용하게 쓰이는 문제들이니 꼭 숙달해둘 필요가 있는 것 같다.😥
5. 문제 추천
https://www.acmicpc.net/problem/16234
16234번: 인구 이동
N×N크기의 땅이 있고, 땅은 1×1개의 칸으로 나누어져 있다. 각각의 땅에는 나라가 하나씩 존재하며, r행 c열에 있는 나라에는 A[r][c]명이 살고 있다. 인접한 나라 사이에는 국경선이 존재한다. 모
www.acmicpc.net
https://www.acmicpc.net/problem/16236
16236번: 아기 상어
N×N 크기의 공간에 물고기 M마리와 아기 상어 1마리가 있다. 공간은 1×1 크기의 정사각형 칸으로 나누어져 있다. 한 칸에는 물고기가 최대 1마리 존재한다. 아기 상어와 물고기는 모두 크기를 가
www.acmicpc.net
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘 (0) | 2022.08.02 |
|---|---|
| [알고리즘] 브루트포스(brute force) 기법 정리 (0) | 2022.02.23 |
| 정렬 알고리즘 정리 (0) | 2021.10.31 |
